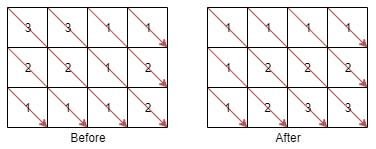
1329. Sort the Matrix Diagonally

Medium

---

A matrix diagonal is a diagonal line of cells starting from some cell in either the topmost row or leftmost column and going in the bottom-right direction until reaching the matrix's end. For example, the matrix diagonal starting from mat[2][0], where mat is a 6 x 3 matrix, includes cells mat[2][0], mat[3][1], and mat[4][2].

Given an m x n matrix mat of integers, sort each matrix diagonal in ascending order and return the resulting matrix.

Example 1:

Input: mat = [[3,3,1,1],[2,2,1,2],[1,1,1,2]]
Output:
 [[1,1,1,1],[1,2,2,2],[1,2,3,3]]

Example 2:

Input: mat = [[11,25,66,1,69,7],[23,55,17,45,15,52],[75,31,36,44,58,8],[22,27,33,25,68,4],[84,28,14,11,5,50]]
Output:
 [[5,17,4,1,52,7],[11,11,25,45,8,69],[14,23,25,44,58,15],[22,27,31,36,50,66],[84,28,75,33,55,68]]

Constraints:

• m == mat.length

• n == mat[i].length

• 1 <= m, n <= 100

• 1 <= mat[i][j] <= 100

class Solution:
    def diagonalSort(self, mat: List[List[int]]) -> List[List[int]]:
        #.
        row, col = len(mat), len(mat[0])
        
        # This diagonal parse logic is important
        for i in range(1, row + col - 2):
            if i < row:
                start_row, start_col = row - i - 1, 0
            else:
                start_row, start_col = 0, i - row + 1
            
            # Add all diagonal elements to arr
            diag = []
            while start_row < row and start_col < col:
                diag.append(mat[start_row][start_col])
                start_row += 1
                start_col += 1
            # Sort array
            diag.sort()
            start_row -= 1
            start_col -= 1
            while start_row >= 0 and start_col >= 0:
                # Add back all sort diagonal elements back
                mat[start_row][start_col] = diag.pop()
                start_row -= 1
                start_col -= 1

        return(mat)