897. Increasing Order Search Tree

Easy

---

Given the root of a binary search tree, rearrange the tree in in-order so that the leftmost node in the tree is now the root of the tree, and every node has no left child and only one right child.

Example 1:

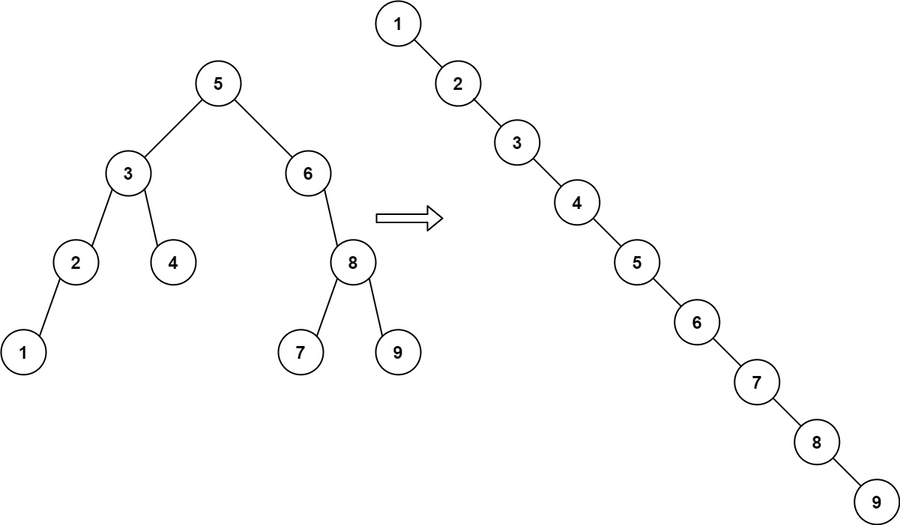
Input: root = [5,3,6,2,4,null,8,1,null,null,null,7,9]
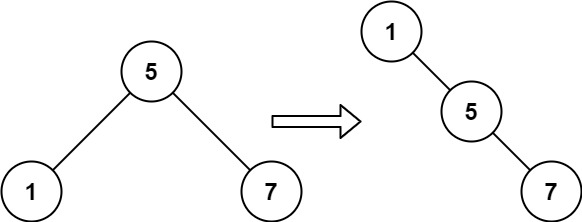
Output: [1,null,2,null,3,null,4,null,5,null,6,null,7,null,8,null,9]

Example 2:

Input: root = [5,1,7]
Output: [1,null,5,null,7]

Constraints:

• The number of nodes in the given tree will be in the range [1, 100].

• 0 <= Node.val <= 1000

Solution 1:

Time Complexity : O(n) Space Complexity : O(n)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def increasingBST(self, root: TreeNode) -> TreeNode:
        values = []
        def recursion(root, values):
            if not root:
                return
            recursion(root.left, values)
            values.append(root.val)
            recursion(root.right, values)
        recursion(root, values)
        return self.build_skewed(values)

    def build_skewed(self, values):
        root = temp = None
        for value in values:
            node = TreeNode(value)
            if root is None:
                root = temp = node
            else:
                temp.right = node
                temp = node
        return root

Solution 2:

Time Complexity : O(n) Space Complexity : O(1)

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def increasingBST(self, root: TreeNode) -> TreeNode:
        def recursion(root):
            if not root:
                return
            recursion(root.left)
            root.left = None
            self.current.right = root
            self.current = root
            recursion(root.right)
        head = self.current = TreeNode()
        recursion(root)
        return head.right