986. Interval List Intersections

Medium

---

You are given two lists of closed intervals, firstList and secondList, where firstList[i] = [starti, endi] and secondList[j] = [startj, endj]. Each list of intervals is pairwise disjoint and in sorted order.

Return the intersection of these two interval lists.

A closed interval [a, b] (with a <= b) denotes the set of real numbers x with a <= x <= b.

The intersection of two closed intervals is a set of real numbers that are either empty or represented as a closed interval. For example, the intersection of [1, 3] and [2, 4] is [2, 3].

Example 1:

Input: firstList = [[0,2],[5,10],[13,23],[24,25]], secondList = [[1,5],[8,12],[15,24],[25,26]]
Output: [[1,2],[5,5],[8,10],[15,23],[24,24],[25,25]]

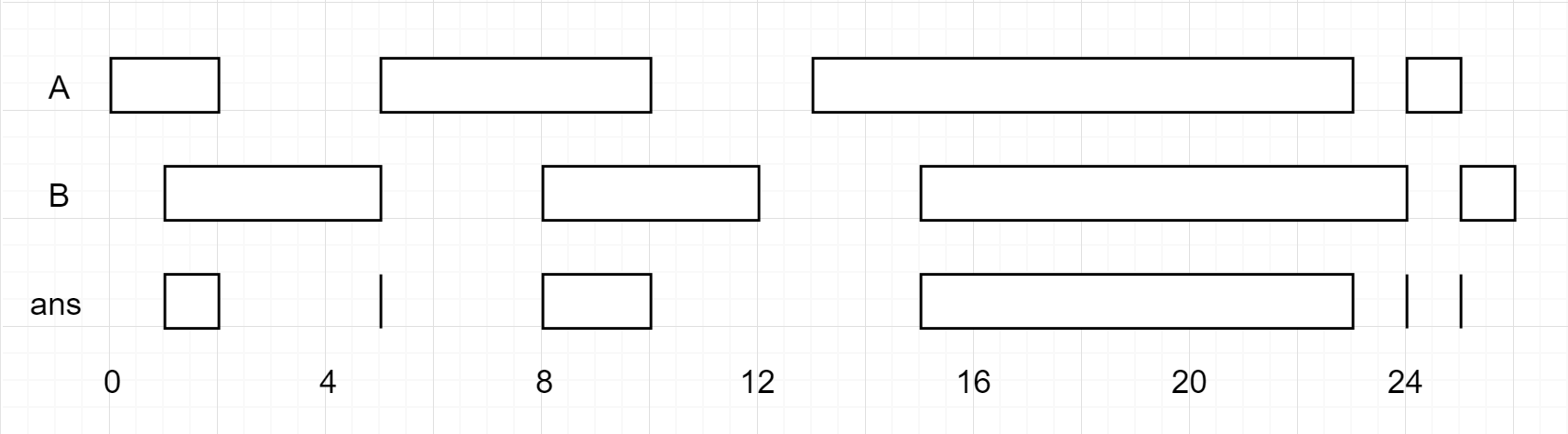
Example 2:

Input: firstList = [[1,3],[5,9]], secondList = []
Output: []

Example 3:

Input: firstList = [], secondList = [[4,8],[10,12]]
Output: []

Example 4:

Input: firstList = [[1,7]], secondList = [[3,10]]
Output: [[3,7]]

Constraints:

• 0 <= firstList.length, secondList.length <= 1000

• firstList.length + secondList.length >= 1

• 0 <= starti < endi <= 109

• endi < starti+1

• 0 <= startj < endj <= 109

• endj < startj+1

class Solution:
    def intervalIntersection(self, firstList: List[List[int]], secondList: List[List[int]]) -> List[List[int]]:
        index1 = 0
        index2 = 0
        result = []
        while index1 < len(firstList) and index2 < len(secondList):
            interval = [max(firstList[index1][0], secondList[index2][0]), min(firstList[index1][1], secondList[index2][1])]
            if interval[0] <= interval[1]:
                result.append(interval)
            if firstList[index1][1] < secondList[index2][1]:
                index1 += 1
            else:
                index2 += 1
        return result